[Deep Learning] Activation Function
Activation function에 대해서 공부해보자.
공부를 하기 전에...
https://operatingsystems.tistory.com/entry/Data-Mining-Artificial-Neural-Network?category=797473
위의 포스팅에서 잘못 써둔 것이 사실 하나 있다.(지금은 고침)
"...가장 일반적으로 sigmoid function을 택한다...."
안된다. 그러면 안된다. 이번 포스팅에서 그 오류를 설명하고 그 대안까지, 전반적으로 Activation Function에 대해서 알아야 할 많은 것들을 다뤄보려고 한다.
위의 포스팅에서 Activation Function이 뭐하는 함수인지 그냥 언급만 했다. 그것이 왜 필요한지 등은 설명하지 않았다. 이번 포스팅에서는 그것을 해보려고 한다. 정답을 우선 말해보자면, Non linear한 데이터의 분포에 대해서도 분류를 해낼 수 있도록 피처를 만들어주기 위해서이다. 무슨 말이냐.. 조금 더 쉽게 설명해보자.
이것을 설명하는데 가장 직관적인 예제는 그 유명한 XOR 문제이다. XOR의 결과 연산을 딥러닝으로 예측하는 문제를 만들어보자. 전체 소스코드는 제일 아래에 github repository에 있으니 읽으시면서 참고하시길 바란다.
'''
XOR Model
'''
import tensorflow as tf
# placeholders for x and y
input_x = tf.placeholder(tf.float32, [None, 2])
input_y = tf.placeholder(tf.int64, [None, 2])
# weight1 and bias1
w1 = tf.Variable(tf.truncated_normal([2, 300], stddev=0.1))
b1 = tf.Variable(tf.constant(0.1, shape=[300]))
z1 = tf.nn.xw_plus_b(input_x, w1, b1)
active1 = tf.sigmoid(z1)
# weight2 and bias2
w2 = tf.Variable(tf.truncated_normal([300, 2], stddev=0.1))
b2 = tf.Variable(tf.constant(0.1, shape=[2]))
z2 = tf.nn.xw_plus_b(active1, w2, b2)
# for test purpose
no_active = tf.nn.xw_plus_b(z1, w2, b2)
sigmoid_active = tf.nn.xw_plus_b(tf.sigmoid(z1), w2, b2)
relu_active = tf.nn.xw_plus_b(tf.nn.relu(z1), w2, b2)
# prediction and training
predictions = tf.argmax(z2, axis=1)
loss = tf.nn.softmax_cross_entropy_with_logits_v2(labels=input_y, logits=z2)
mse = tf.reduce_mean(loss)
train = tf.train.GradientDescentOptimizer(0.1).minimize(mse)위의 모델은 가장 일반적인 형태의 fully-connected network이다. 주목할 부분은 active1이다. active1을 sigmoid(z1)으로 할 때와 그냥 z1으로 할 때를 비교해보자. 결론부터 말하면 active1 = tf.sigmoid(z1)은 xor 모델 학습이 되고, active1 = z1은 학습 자체가 안된다.
그럼 왜 안되는지를 설명해보자. 우선 어려운 말보다는 쉽게 그림으로 설명해보려고 한다. sigmoid(z1)을 통해서 z2 값이 어떤 분포로 나타나게 되는지를 봐보자.
# 학습하는 부분 코드
import numpy as np
import tensorflow as tf
steps = 10000
bchsize = 256
def generator(train_x, train_y, bchsize=bchsize):
start = 0
while True:
if start > len(train_x):
start %= bchsize
batch_x = train_x[start:start+bchsize]
batch_y = train_y[start:start+bchsize]
start += bchsize
yield batch_x, batch_y
# shuffle dataset
random_idx = np.random.choice(len(x), (len(x)), replace=False)
x, y = x[random_idx], y[random_idx]
# split train/test dataset
n_train = int(len(x)*0.8)
train_x, train_y = x[:n_train], y[:n_train]
valid_x, valid_y = x[n_train:], y[n_train:]
valid_y = np.argmax(valid_y, axis=1)
# make generator
gen = generator(train_x, train_y)
# global variable initialization
init = tf.global_variables_initializer()
train_ops = [loss, mse, train]
transform_ops = [no_active, sigmoid_active, relu_active, predictions]
with tf.Session() as sess:
# initialization
sess.run(init)
# do training
for i in range(steps):
bx, by = next(gen)
feed_dict = {
input_x: bx,
input_y: by
}
train_loss, train_mse, _ = sess.run(train_ops, feed_dict=feed_dict)
if i % 1000 == 0:
pred = sess.run(predictions, feed_dict={input_x: valid_x})
acc = (valid_y == pred).astype(int).mean()
print('%sth iteration finished: %.4f, validation_accracy: %.4f' % (i, train_mse, acc))
# transform data
feed_dict = {input_x: x}
no_active_x, sigmoid_active_x, relu_active_x, pred_x = sess.run(transform_ops, feed_dict=feed_dict)
print(no_active_x.shape, sigmoid_active_x.shape, relu_active_x.shape, pred_x.shape)
학습이 끝난 후에 전체 데이터 x에 대해서 z2값을 구하고, 그것을 plot해보니 아래와 같은 결과가 나왔다. 원래의 데이터 분포, active1 = tf.sigmoid(z1)과 active1 = z1 둘의 결과를 비교해보자.
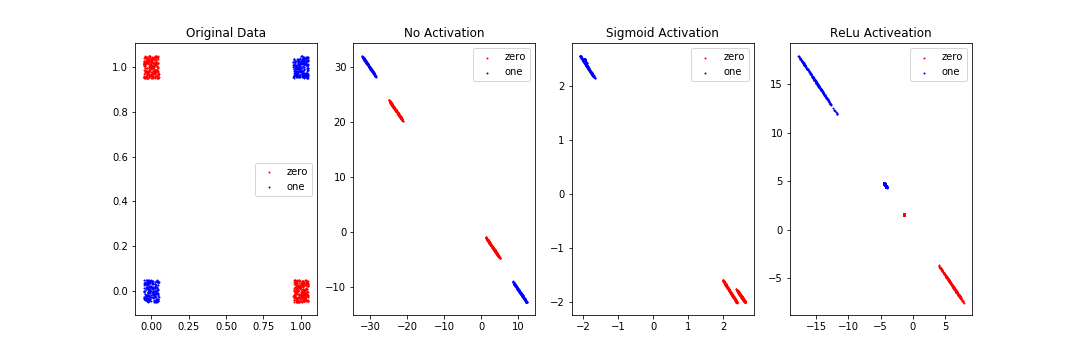
Original Data, No Activation은 선 하나로 나눌 수 없게 돼 있고, Sigmoid Activation과 ReLu Activation은 나눌 수 있게 돼 있다. 왜 그럴까? 일단 가장 큰 차이는 activation function의 유무이다. 기본적으로 2차원 데이터를 평면 상에 나타냈을 때(Original Data)는 선 하나로 나눌 수 없는 형태이다. 그래서 모델 학습을 진행하는데, activation 함수를 적용하지 않았더니(No Activation) 학습을 하나 마나였다는 것이다. 그런데 activation 함수를 적용을 하니(Sigmoid Activation, ReLu Activation) 선 하나를 이용해서 둘로 나눌 수 있는 형태가 됐다는 것이다.
종합하면, 다음과 같은 결론이 나온다. xor 데이터의 0과 1을 선 하나로 구분하는 것은 불가능하다. 그래서 우리는 sigmoid, relu와 같은 함수를 중간에 적용해준다. 그러면 선 하나로 구분할 수 있는 형태로 변형이 가능하다. 여기서 "선 하나로"라고 계속 이야기하는 것을 조금 유식하게 말하면 linear하게(=선형적으로)이다. 즉 xor 데이터는 선형적으로는 구분을 할 수 없으니, 비선형 함수인 sigmoid, relu함수 등을 사용해서 학습해주면 된다는 것이다. 이 비선형 함수를 적용한 결과가 위의 가운데 그림인 것이다.
자 이제, activation 함수를 왜 사용하는지 알아봤다. 이걸 사용해야 선형으로 나눌 수 없는 모델을 나눌 수 있게 되기 때문이다. 그럼 이제 어떤 activation 함수들이 있는지와 그것들의 특징에 대해서 알아보자.
이 부분을 이야기하기 전에 2000년 이전에 딥러닝이 발전하지 않았을 때 사용했던 Activation 함수들에 대해서 이야기를 먼저 해보려고 한다. sigmoid, tahn 함수들이 바로 그것들이다. 이 함수들은 각각 아래와 같은 모양으로 그래프를 그릴 수 있다.
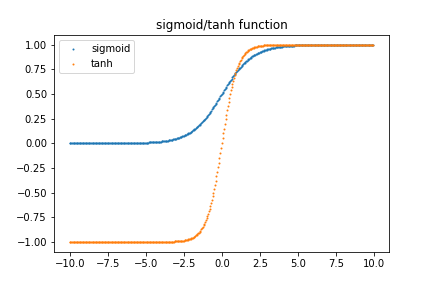
두 함수의 공통점은 뭘까? 음/양 무한대로 가면 값이 거의 똑같다는 것이다. 이는 두 함수를 미분했을 경우, 음/양 무한대의 미분값은 거의 0이라는 뜻이다. 이것이 딥러닝의 학습 과정에서 영향을 주는 것이 그 유명한 Gradient vanishing problem이다. Gradient vanishing problem에 대해서는 다음에 자세하게 포스팅하려고 하는데, 여기서는 간단하게 이렇게만 설명하고 넘어가보자. 딥러닝 학습 과정은 기본적으로 cost function을 최소화하는데 있다. 어떤 함수의 최소값을 구할 때 우리는 고등학교 때 미분을 하곤 했다. 즉, 딥러닝 학습 과정을 거치기 위해서는 미분 과정을 거쳐야 하는데, sigmoid와 tahn 함수를 미분할 경우에는 x 값이 음/양 무한대로 가면 갈수록 미분 값이 0이 되고, 그 결과 학습되는 양이 거의 0에 수렴하게 된다. gradient가 기울기, 즉 미분 값을 의미하는데 그 값이 사라지는 문제. 그것이 gradient vanishing problem이다. (여기에서는 이렇게 간단하게만 이야기하고 이것에 대해서는 자세하게 다음에 포스팅하려고 한다.)
여기서 재미있는 인터뷰 영상을 하나 보자.
https://www.youtube.com/watch?v=pnTLZQhFpaE
3:00 정도에 Andrew님께서(동양분) Yoshua께(서양분) 이렇게 질문한다.
Andrew: .... 예전에 했었던 가장 큰 실수가 있다면 어떤 것이 있을까요??
Yoshua: ... 예전에는 당연히 선형적이지 않은 부분을 smooth하게 해야 된다고 생각했다. 그런데 2010년도에 와서 보니까 ReLU와 같은 non-linear한 형태의 activation 함수가 잘 동작한다는 것을 알게 됐다. ...
이런 대화를 한다. 이 대화를 여러 각도에서 생각해볼 필요가 있다. 우선, 저렇게 똑똑한 분들이 지난 몇 십년동안 당연하다고 생각했던 것도 틀릴 수 있다는 것이다. 그러니까 Yoshua님도 big surprise로 이것을 든 것이다. (과연 우리가 지금 당연하게 알고 있는 것들도 그런 것들이 있을 수 있을까? maybe?)
이 분들의 인터뷰 영상을 연결고리로 해서 ReLU에 대해서 이야기해보려고 한다. ReLU는 Rectified Linear Unit의 약자이다. Rectified는 교정된이라는 뜻이다. 그렇다면, "수정된 선형 유닛"정도로 억지 번역될 수 있겠다. 우선 ReLU 함수를 그려보자.
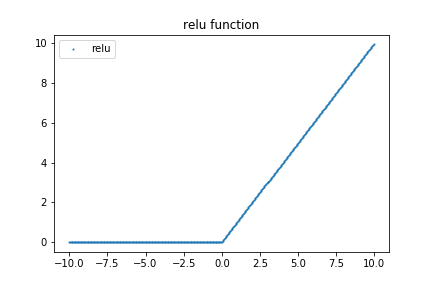
"이렇게 하면 안 될것이다"라고 Yoshua님께서 젊었을 때 생각하셨단다.
Yoshua: 이렇게 하면 너무 많은 부분에서 0이 나오게 되기 때문에 학습에 방해된다. 따라서 이렇게 하면 아니되오!! 라고 생각했다. 그런데 2010년 이후에 확인해보니, 실제로 이렇게 학습하는 것이 훨씬 잘 학습을 한다는 것을 발견했다.
ReLU 함수는 computation 역시 빠르게 가능하다. max(x, 0)가 전부이다. 즉, 0보다 크면 x, 그렇지 않으면 0이므로, 단순 if-else 문으로 구현할 수 있는 함수이다. 그렇다면 ReLU의 단점은 뭘까? dying problem이 있다. Yoshua님께서 걱정했듯이, 학습 시에 많은 부분이 0이 되버리는(die) 문제이다. 이런 문제점을 해결하기 위해 나온 ReLU 변형은 아래에 가볍게 리스팅만 해두려고 한다.
- leaky ReLU
- maxout (ReLU와 leaky ReLU를 같이 고려해서 만듬)
자, 그래서 어떤 activation 함수를 골라야 할까? 사실 답은 없다. Yoshua님께서 깨닳으신데로 우리가 당연히 그것이 맞다라고 생각한 것도 틀릴 수 있는 것이다. 그렇지만 보통 여러 사람들이 일반적으로 하는 말은, "모르면 ReLU를 써라"이다. 일반적으로 sigmoid나 tanh 보다는 좋다고 한다.
# Reference
https://towardsdatascience.com/activation-functions-and-its-types-which-is-better-a9a5310cc8f
# github repository
https://github.com/jinkilee/operatingsystems.tistory.com/tree/master/source/blog_1